第一章 函数与极限 #
极限存在的充要条件是左右极限都存在且相等
映射与函数 #
偶函数: f(-x) = f(x)
奇函数: f(-x) = - f(x)
反函数 对任意 y 都有唯一确定的 x 使得 y = f(x), 这样的函数才有反函数 $x = f^{-1}(y)$, 函数和反函数的图形关于 y = x 对称
复合函数需要注意内层值域和外层定义域相交
基本初等函数: 幂函数, 指数函数, 对数函数, 三角函数, 反三角函数
初等函数: 由常数和基本初等函数经过有限次加减乘除和复合所得到且能用一个解析式表达的函数

习题P16: 6,7(4)(5)(6), 8, 9(1)(2)(5), 12, 13
数列的极限 #
研究问题往往从特殊到一般, 我们通过研究数列的极限进而逼近函数的极限

习题P26: 2,3,6,7,8
函数的极限 #

同样的, 函数的极限同样具有唯一性, (局部)有界性, (局部)保号性
习题P33: 4, 11, 12
无穷小与无穷大 #
无穷小的定义:

无穷大的定义:

极限运算法则 #
注意极限运算法则要求拆分后的部分极限也存在


极限存在法则 #
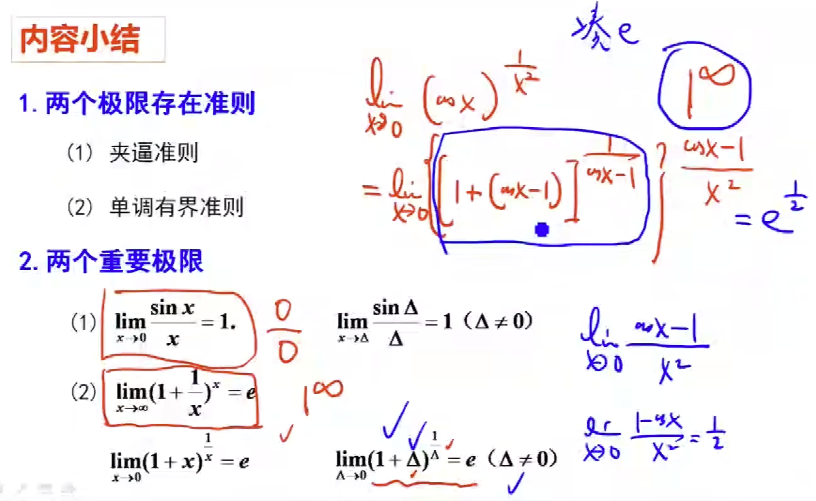
习题P52: 1(4,5,6), 2(2,3), 4(2,3,5)
无穷小的比较 #
指数函数, 只要指数大于 0, 趋势就比 lnx 快, 可以用洛必达法则推导
注意等价无穷小替换只适用于乘除不适用于加减

重要等价无穷小的证明:

常用的等价无穷小:

注意这里的换元用法, 任意趋向于 0 的自变量都成立:
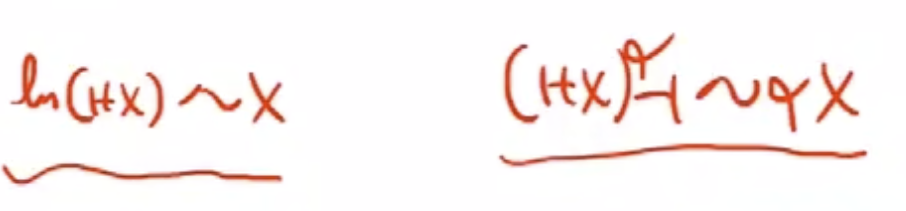
x 趋向于 0 时常用的等价无穷小:
- ln(1+x) ~ x
- $(1+x)^{\alpha} - 1$ ~ $\alpha x$ 也即 ($\sqrt[n]{1+x} - 1$ ~ $\frac{1}{n}x$)
- x ~ sinx ~ tanx ~ arcsinx ~ arctanx
- 1 - cosx ~ $\frac{1}{2}x^2$
- $e^x - 1$ ~ x
等价无穷小在加减法中能否运用要开具体的泰勒展开式(即等价无穷小是泰勒展开的粗浅近似运用)
习题P55: 4,5,6
函数连续性与间断点 #

习题P61: 3,4,5,6
连续函数的运算与初等函数的连续性 #




习题P65: 3(7,8), 4(4,5,6,7), 5
1.10 闭区间上连续函数性质 #


