第二章 导数与微分 #
导数 #
导数存在的充要条件 <=> 左右导数存在且相等 (尤其是分段函数)

可导一定有切线,但有切线不一定可导, 如 $f(x) = x^3$
初等函数在定义域上都是连续可导的

习题P83: 4,5,6,7,13,16,17,18
函数的求导法则 #
有理运算(和差积商)法则:

反函数的运算法则:

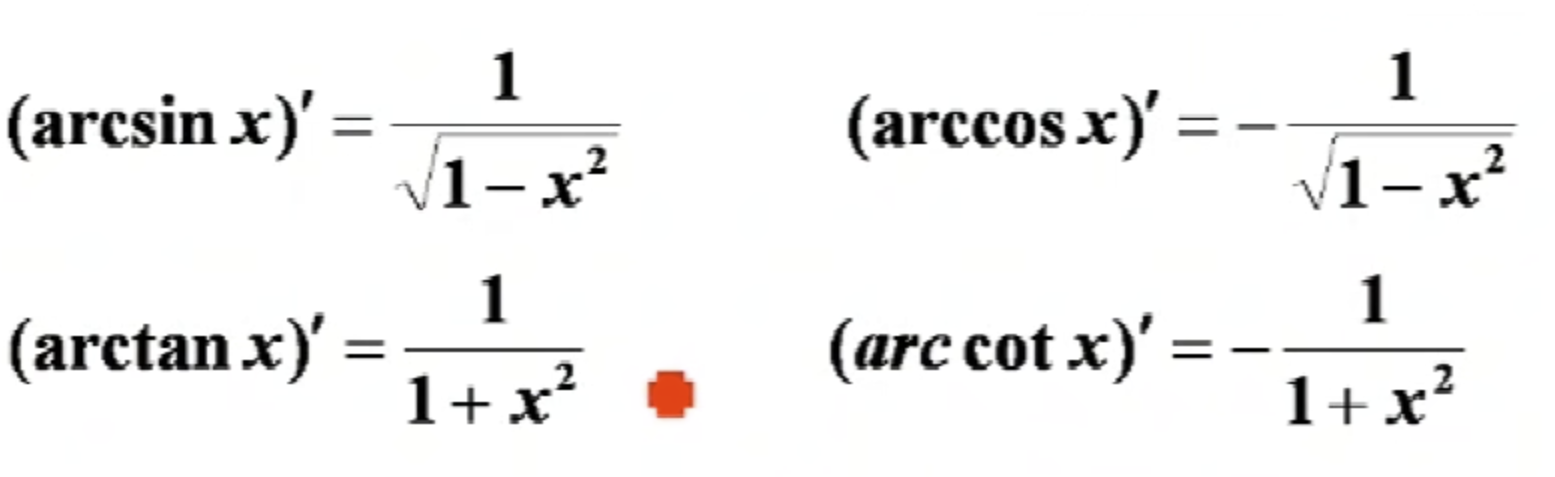
常见的反三角函数导数:
复合函数的求导法则:

常见的基本初等函数的导数公式:

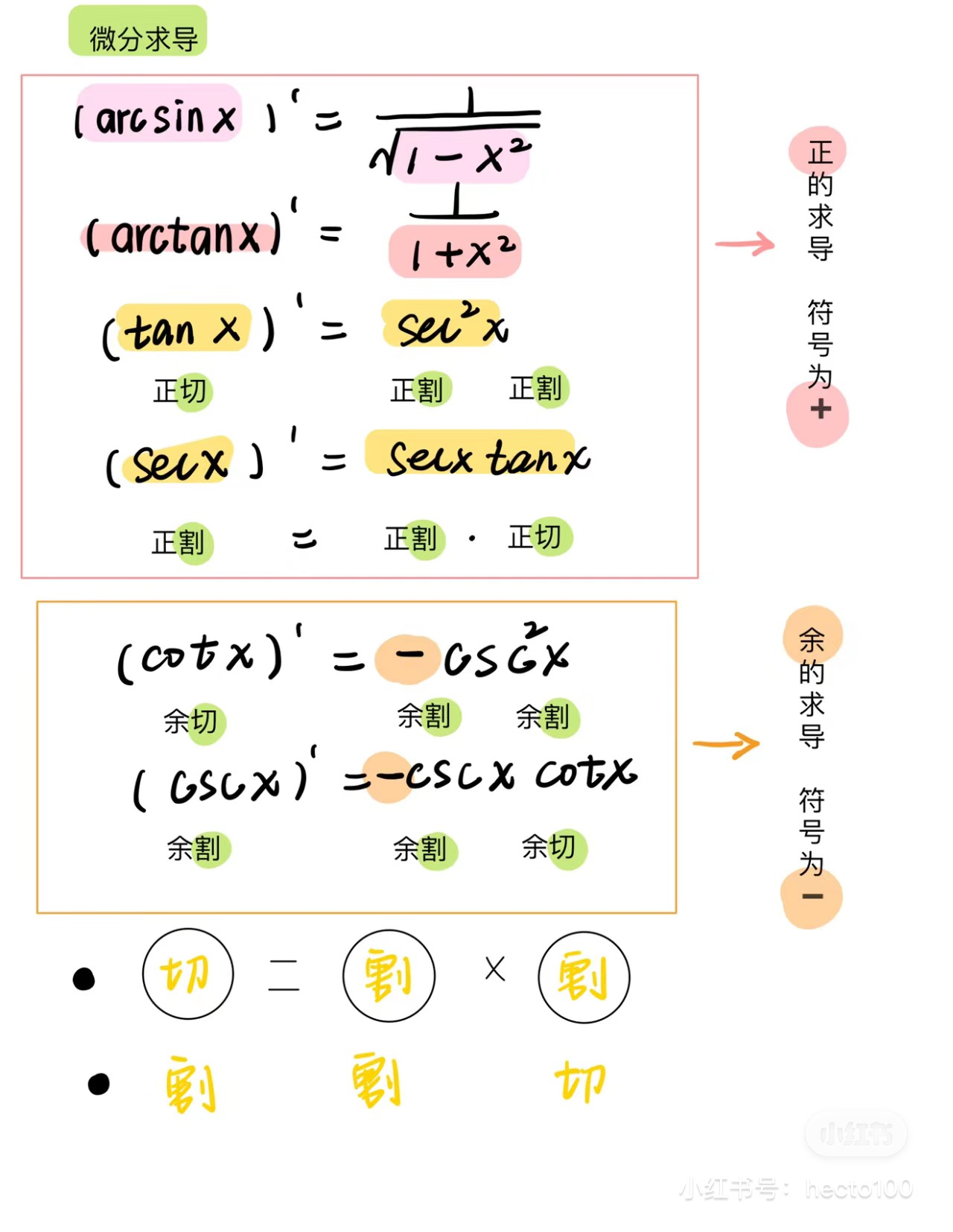
常见三角函数导数助记:
非基本初等函数就换成基本初等函数,例如指数+幂数(幂指函数), 两边同时取对数
习题P94: (6,7,8)中单号小题, 9, 14
高阶导数 #
3阶以下用y’‘‘区分,4阶及以上用y(n)表示
求法:
- 归纳法, 例如 sinx’ = sin(x + nΠ/2)
- 和差公式, 乘积公式(Leibniz公式), 尽量用和差(简单,可以考虑拆项实现)
- 泰勒公式

习题: P100: 2,3,4,10,11
隐函数及参数方程的导数 #
隐函数 F(x, y) = 0 显化为 y = f(x) 后求导方法:
- 原式对 x 求导
- 对数求导法(可以将乘除变为加减,不能确定正负的时候记得加绝对值)
习题P108: 2, 3(3)(4), 4(1)(3), 8(3)(4), 11
函数的微分 #
微分 dy 是 Δy 的线性主部![微分的定义]!(1729180018842.jpg) 可微 <=> 可导
微分的几何意义: 曲线的切线增量近似代替曲线的增量
积分函数的微分公式 y = f’(x) * dx
四则运算法则同导数四则运算
复合函数微分法则: 微分形式不变性 dy = 微分导数 * 微分

习题P120: 2, 3(2)(4)(6), 4(1)(3)(5)(7)