微分中值定理与导数应用 #
微分中值定理 - 用导数研究函数 #
罗尔定理-最特殊: #
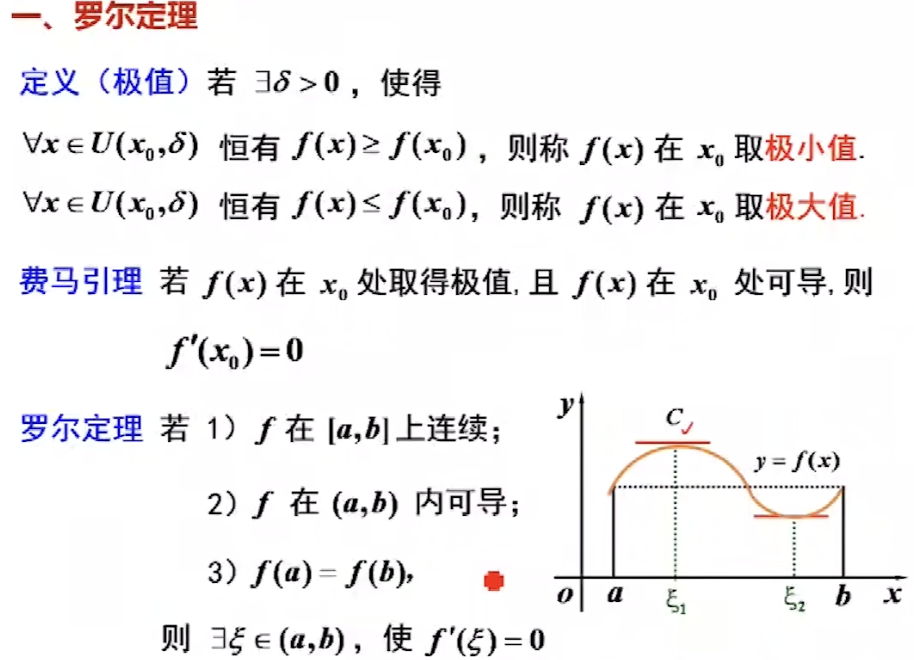
拉格朗日中值定理-特殊: #

注意其(2)推广:
$f(b) - f(a) = f’[a + \theta(b - a)](b - a) (0 \lt \theta \lt 1)$
$f(x_0 + \Delta x)-f(x_0) = f’[x_0 + \theta \Delta x]\Delta x$
拉格朗日定理证明的一个重要不等式: sinx < x < tanx, x属于(0, 2/Π)
例题-发现 $f(a) - f(b) = a - b$ 型不等式, 优先联想到拉格朗日定理:

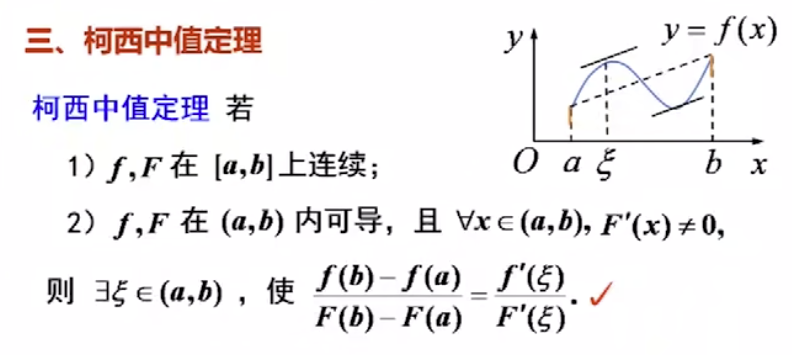
柯西中值定理-一般: #
内容小结 #
闭区间连续, 考虑:
- 介质定理(函数值最大和最小值区间内都能被取到)
- 最值定理(连续函数在闭区间上可以取到最大值与最小值)

P132, 5-12(除9)
(进阶)微分方程解法 #

构造 $F(X) = f(x)e^{\int P(x)dx} - \int Q(x)e^{\int P(x)dx}dx$
例题1:

例题2:

例题3-二阶降阶(即求一阶导函数):

例题4-二阶降阶先拉格朗日后罗尔定理:

例题5-非标准自变量

三阶考虑泰勒?
洛必达法则 - 借助导数研究 0 / 0 的极限(∞ / ∞ 也可) #
注意使用前提: 导数的极限要存在(或 ∞)

例题-常规:
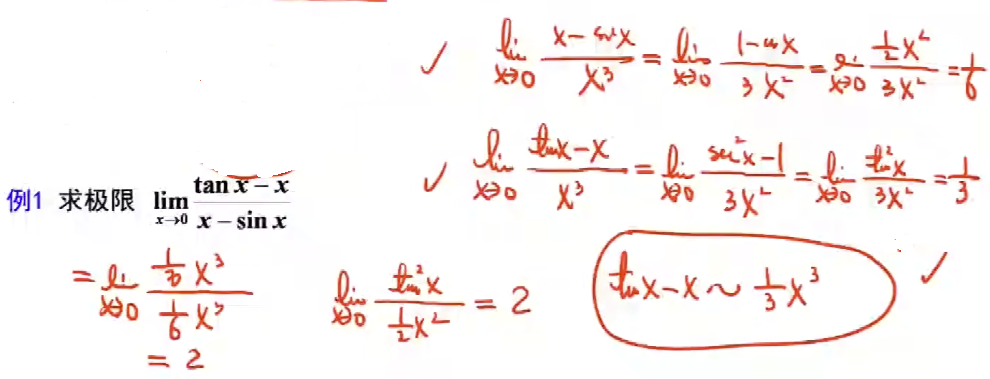
例题2 - $\frac{0}{0}$ 型, 可直接洛必达, 注意利用等价无穷小化简:
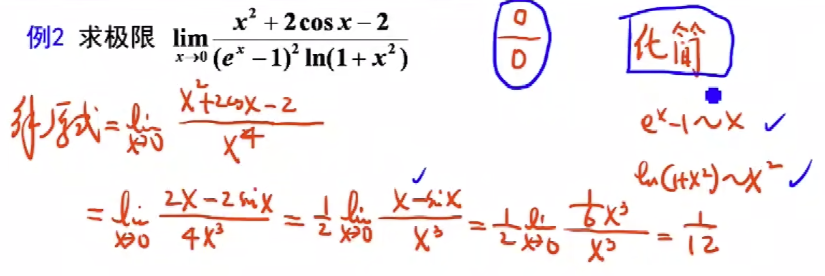
例题3 - $\frac{\infin}{\infin}$ 型, 可直接洛必达:

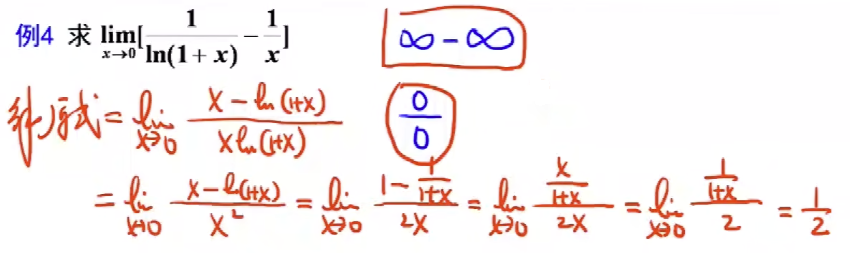
例题4 - $\infin - \infin$ 型, 通分化为 $\frac{0}{0}$:
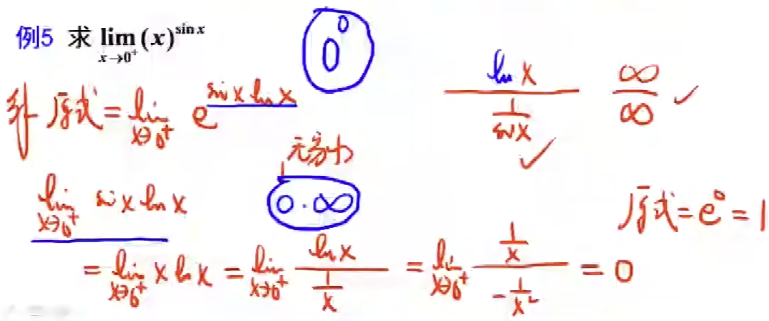
例题5 - $0^0$ 型,幂指函数改写为指数函数变成 $0 \cdot \infin$, 再转换为两种基础形式:
例题6 - $1^{\infin}$, 转换为 $0 \cdot \infin$, 后续视难易转换为两种基础形式:

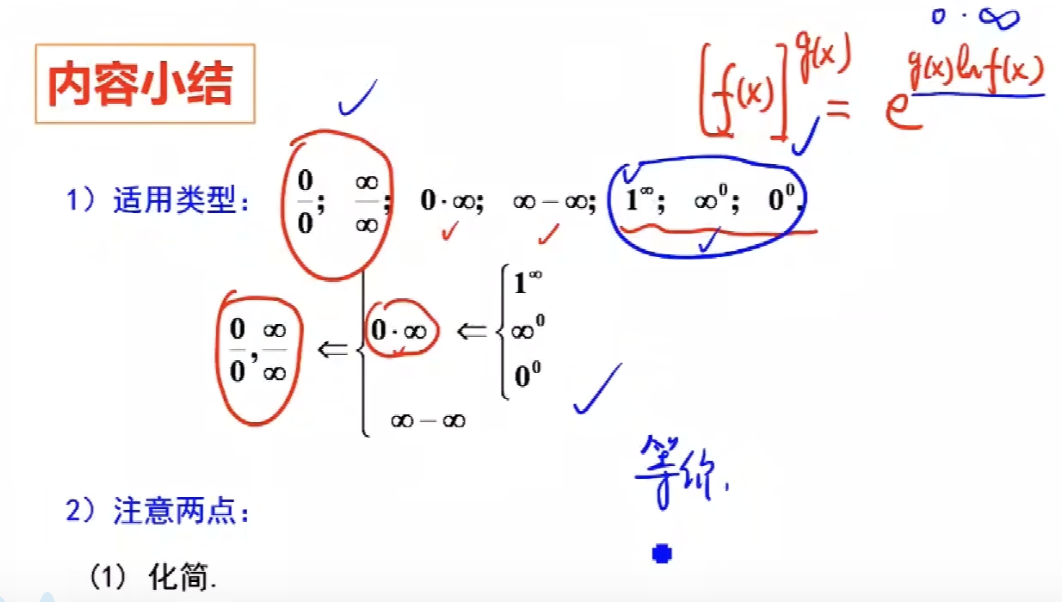
内容小结:
P137: 1(3)(5)(9)(11)(13)(15)(16); 2; 3
泰勒公式 - 函数和高阶导数间的关系 #
$f(x) = f(x_0) + f’(x_0)(x-x_0) + \frac{f’’(x_0)}{2!}(x-x_0)^2 + \cdots$
泰勒公式: 函数 = n 阶多项式 + 余项
意义:
- 用多项式逼近, 用余项表示误差
- 将函数和其高阶导数联系在一起
泰勒公式的几何意义:
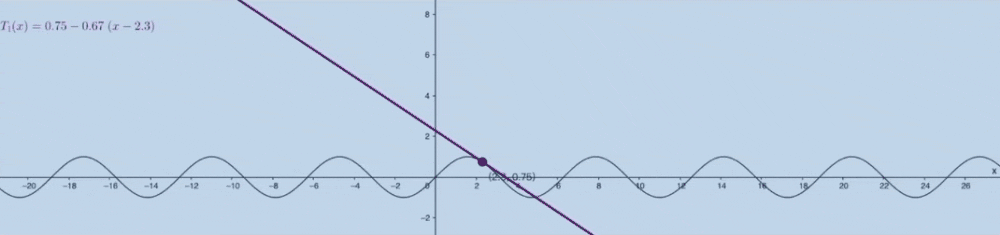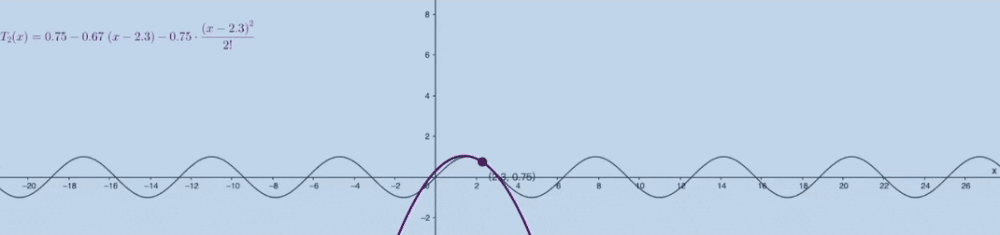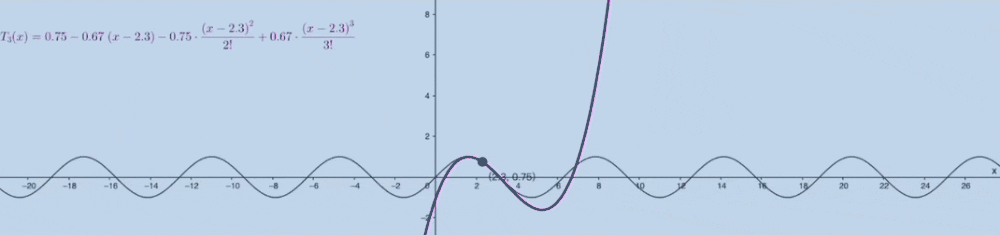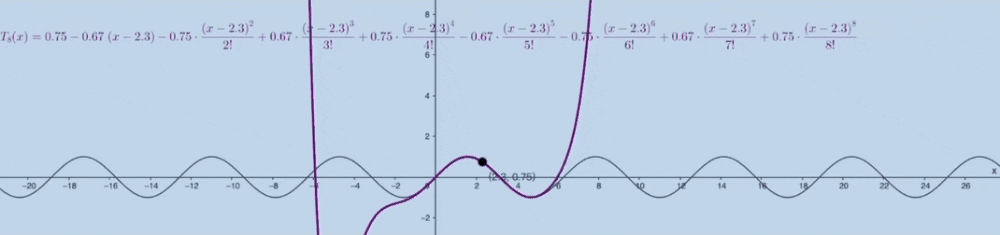
麦克劳林公式 #
即泰勒公式在 0 点($x_0 = 0$)的展开:
$f(x) = f(0) = f’(0)x + \frac{f’’(0)}{2!} + \cdots + \frac{f^{(n)}(0)}{n!}x^n + \cdots$
记忆方式:
- 第一项联想到等价无穷小(如: $e^x - 1 \sim x, sinx \sim x$)
- 奇偶性(如 $sinx$ 奇函数奇次方, $cosx$ 偶函数偶次方)
- 根据已有求导/积分
- 等比数列求和如: $a_1\frac{1 - q^n}{1-q}$, x 趋向于零即 $\frac{1}{1-x} = 1 + x + x^2 + \cdots$
常用的泰勒公式(0点展开, 麦克劳林公式):
第一组:
$e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots$
第二组:
$sinx = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots$
求导得出:
$cosx = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \cdots$
与 1 式相比, 正负5次方(因此 arcsinx > sinx)
$arcsinx = x + \frac{x^3}{6}$
第三组:
$\frac{1}{1-x} = 1 + x + x^2 + x^3 + \cdots$
由 1 式令 t = -x 得到:
$\frac{1}{1+x} = 1 - x + x^2 - x^3 + \cdots$
由 1 式令 $t = -x^2$ 得到:
$\frac{1}{1+x^2} = 1 - x^2 + x^4 - x^6 + \cdots$
由 2 式积分得到:
$ln(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \cdots$
由 3 式积分得到:
$arctanx = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \cdots$
与 1 式相比, 正负三次方:
$tanx = x + \frac{x^3}{3}$
级数求和常用的泰勒展开:
- $\frac{x}{1-x} = x + x^2 + x^3 + \cdots + x^n = \displaystyle \sum_{n=1}^{\infin}x^n$
- $\frac{x}{(1-x)^2} = x + 2x^2 + 3x^3 + \cdots + nx^n = \displaystyle \sum_{n=1}^{\infin}nx^n$
- $\frac{x}{(1+x)^2} = 1 - x^2 + x^4 - x^6 \cdots + (-1)^nx^{2n} = \displaystyle \sum_{n=0}^{\infin}(-1)^nx^{2n} = (arctanx)'$
- $\frac{x}{(1+x)^2} = x - \frac{x^3}{3} + \frac{x^5}{5} - - \frac{x^7}{7} \cdots + \frac{(-1)^n}{2n+1}x^{2n} = \displaystyle \sum_{n=0}^{\infin}\frac{(-1)^n}{2n+1}x^{2n} = arctanx$
- $ln(1+x) = \displaystyle \sum_{n=0}^{\infin}\frac{(-1)^{n-1}}{n}x^n$
泰勒公式展开多少阶: 表达式中出现的最高阶数,展开项可能出现的所有组合

例题1 - 常规套公式:
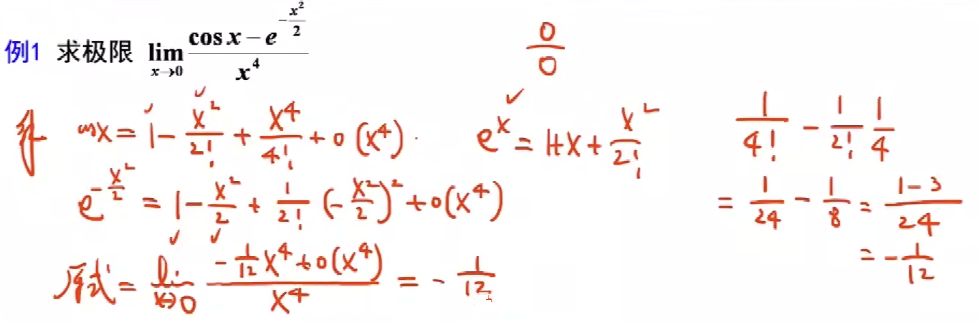
例题2 - 高阶导数证函数值,联想到泰勒(研究局部用佩亚诺余项 , 研究整体用拉格朗日余项?):

例题3 - 求高阶导数例子:
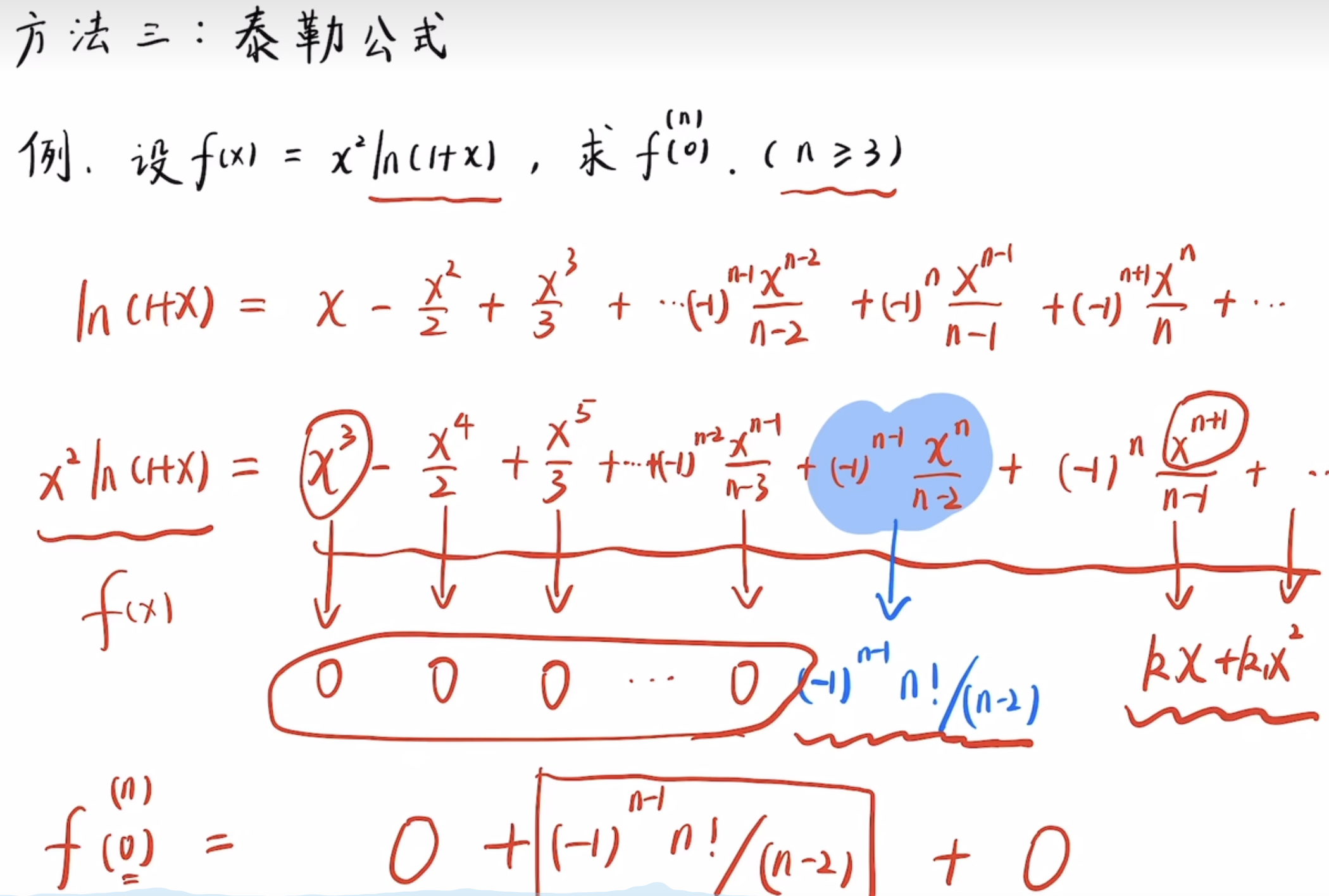
$x_0 = 0$ 时的泰勒公式被称为麦克劳林公式
习题P143: 4, 5, 10(1, 3)
皮亚诺余项 #
$f(x) = f(x_0) + f’(x_0)(x-x_0) + \cdots + \frac{f^{(n)}(x_0)}{n!}(x - x_0)^n + R_n(x)$
其中: $R_n(x) = o(x-x_0)^n$
又叫局部泰勒公式, 主要用于研究局部问题, 如极限/极值
因此只要求在 $x_0$ 处可导
拉格朗日余项 #
$f(x) = f(x_0) + f’(x_0)(x-x_0) + \cdots + \frac{f^{(n)}(x_0)}{n!}(x - x_0)^n + R_n(x)$
其中: $R_n(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!}(x - x_0)^{n+1}, (x \rightarrow x_0)$
又叫整体泰勒公式, 研究整体问题, 如(区间)最值/不等式(注意绝对值不等式放缩)
因此要求在区间上连续可导
若 $x_0 = 0$, 则得麦克劳林公式
带拉格朗日余项的一阶泰勒公式 #
存在二阶连续导数即联想到带拉格朗日余项的一阶泰勒公式:
$f(x) = f(c) + f’(c)(x - c) + \frac{f’’(\xi)}{2!}(x-c)^2, \xi \in (x_0, x)$

泰勒公式在何处展开(即确定 c):
- 中点
- 端点
- 特殊点
- 哪一点的信息多
2001 年真题 #

第一问可用拉格朗日中值定理的2式推广:
$f(b) - f(a) = f’[a + \theta(b - a)](b - a) (0 \lt \theta \lt 1)$
第二问:

2023 年真题 #
函数单调性与曲线凹凸性 #
$f^{’}(x) >= 0$ 则单调增(0点有限个), 可利用该特性证明不等式(一阶为0则二阶)
例题1 - 利用单调性证明不等式(不等式的另一种解法: 拉格朗日):

曲线凹凸性:

拐点 凹凸性发生变化的点; 或二阶导为 0 但三阶导不为 0 的点
可能的拐点:
- $f^{’’}(x) = 0$ 的点
- $f^{’’}(x)$ 不存在的点

习题P150: 3(2)(4)(7), 4, 5(2)(4), 6, 10(1)(2), 11(3), 13, 14, 16
函数的极值与最值 #
驻点:函数的一阶导数为0的点(驻点也称为稳定点,临界点)。对于多元函数,驻点是所有一阶偏导数都为零的点
极值点不一定是驻点(除非可导)。如y=|x|在0点处不可导但是极小值
极值可能点:
- f’(x) = 0(必要非充分条件)
- f’(x) 不存在的点
极值(充分)定理:
- 一阶导数为 0 时, 根据导数正负号变化判断极大极小, 由负转正为极小值,由正转负极大值
- 一阶导数为 0 时, 根据二阶导数正负号判断极大极小, 正为极小值,负为极大值
最大最小值问题(前置条件: 建立目标函数):
- 求驻点和不可导的点
- 求两端点f(a), f(b)
- 比较以上各点函数值
证明不等式的三种方法:
- 最值极值
- 单调性
- 拉格朗日中值定理

习题P161: 1(1,3,8,9), 3, 6(2), 11, 15
函数图形的描绘 #
利用导数描绘函数图形的步骤:
- 确定定义域, 考察奇偶性和周期性
- 求一阶导和二阶导, 并求出 f’(x) 和 f’’(x) 为 0 和不存在的点
- 列表判别增减和凹凸区间,求出极值和拐点
- 求渐进线
- 水平渐近线: $\lim_{x \rightarrow \infin} f(x) = A$, y = A 是水平渐近线
- 垂直渐近线: $\lim_{x \rightarrow x_0}f(x) = \infin, x = x_0 是垂直渐近线$
- 斜渐近线:
- $\lim_{x \rightarrow \infin}\frac{f(x)}{x} = a$
- $b = \lim_{x \rightarrow \infin}(f(x) - ax)$
- y = ax + b 是斜渐近线
- 确定某些特殊点, 描绘函数图形

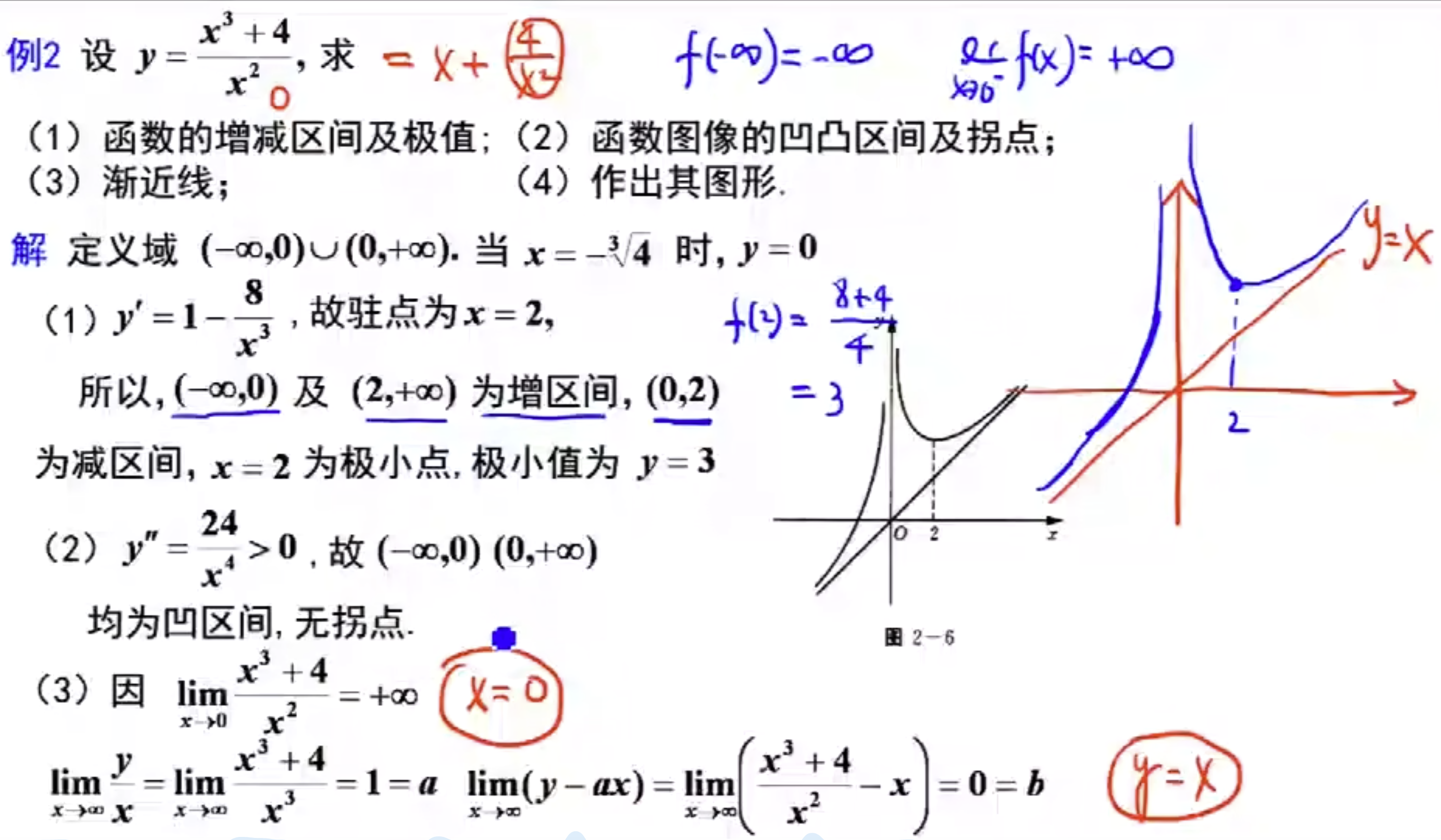
习题P167: 1,4
曲率 #
弧微分:
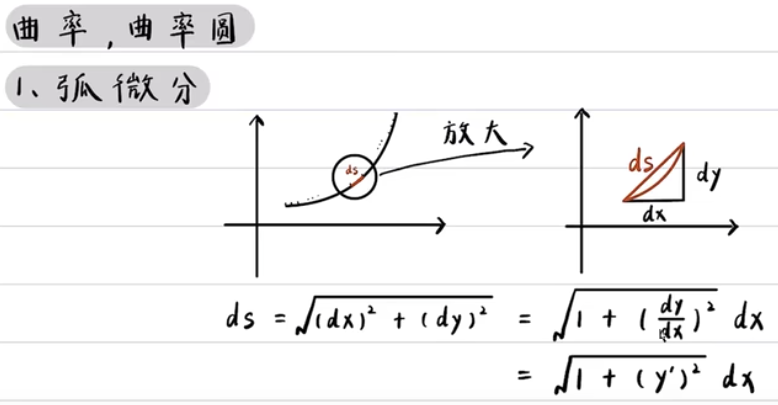
曲率: 通俗的说就是曲线的弯曲程度, 分为:
- 平均曲率: 单位弧长转过的角度
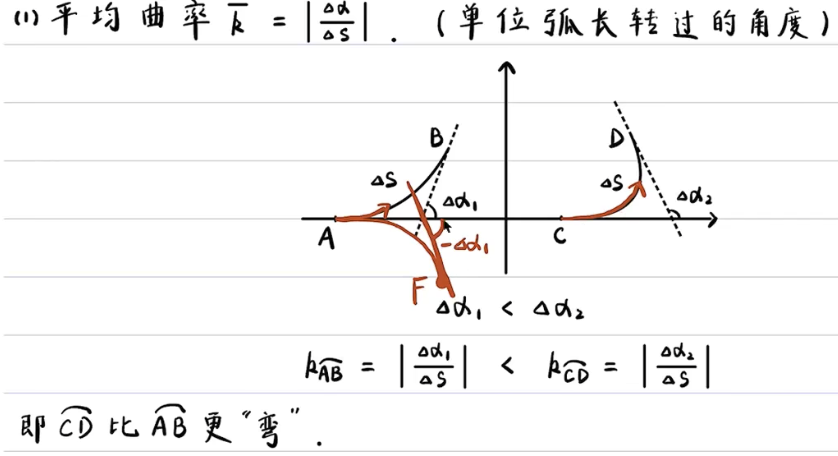
- 某点曲率
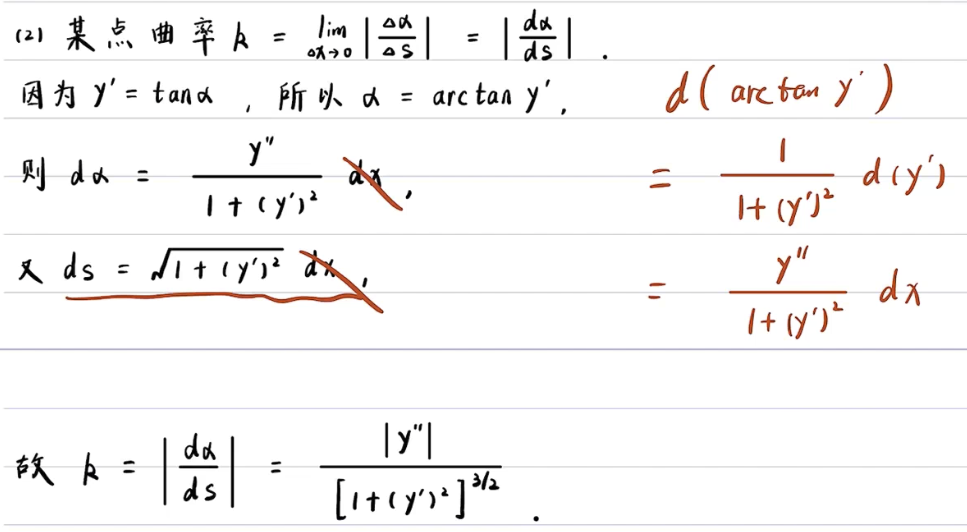
曲率圆: 某点邻域与曲线拟合的最好的圆(相对应的, 多项式的拟合是泰勒公式)
曲率半径 $R = \frac{1}{曲率k}$

考研真题(y极限不存在可 x/y 互换):

拉格朗日中值定理中 $\theta$ 的处理:
- 如果 f(x) 已知, 可以求出来
- 如果未知, 考虑泰勒展开:
- 若 $f’’(x) 连续, 有 f(x) = f(0) + f’(0)x + \frac{f’’(0)}{2!} + 0(x^2)$
例题(2)问: