定积分 #
定积分是一种求和运算(不定积分是反导数运算), 求给定函数在有限区间里与X轴围成图形的面积的定值
定积分的换元法和分部积分法 #
定积分中值定理: $\int_a^bf(x)dx = f(\xi)(b-a)$
积分可以拆开积: $\int_0^1 (a + b) = \int_0^1 a + \int_0^1 b$
定积分的分部积分法(P252):
$\int_a^budv = [uv]_a^b - \int_a^bvdu$
一些常用结论: 若 $f(x)$ 在 [-a, a] 上连续且为偶函数, 则:
$\int_{-a}^ax{\rm d}x = 2\int_0^af(x)dx$
若 $f(x)$ 在 [-a, a] 上连续且为奇函数, 则:
$\int_{-a}^ax{\rm d}x = 0$
设 $f(x)$ 在 [0, 1]上连续:
-
$\int_0^{\frac{π}{2}}f(sinx)dx = \int_0^{\frac{π}{2}}f(cosx)dx$
-
$\int_0^πxf(sinx)dx = \frac{π}{2}\int_0^πf(sinx)dx$
点火公式/华里士公式
$$ I_n = \int_0^{\frac{π}{2}}sin^nxdx = \int_0^{\frac{π}{2}}cos^nxdx $$
- n为正偶数: $\frac{(n-1)}{n} * \frac{(n-3)}{(n-2)} * .. * \frac{3}{4} * \frac{1}{2} * \frac{π}{2}$
- n为大于1的正奇数: $\frac{(n-1)}{n} * \frac{(n-3)}{(n-2)} * .. * \frac{4}{5} * \frac{2}{3}$
注: 0 ~ π 积分为 0 ~ π/2 的二倍, 若因子为 x/2,可令 u = 2 / x 换元
积分上限的函数及其导数 #
ref
定积分上限函数及其导数:
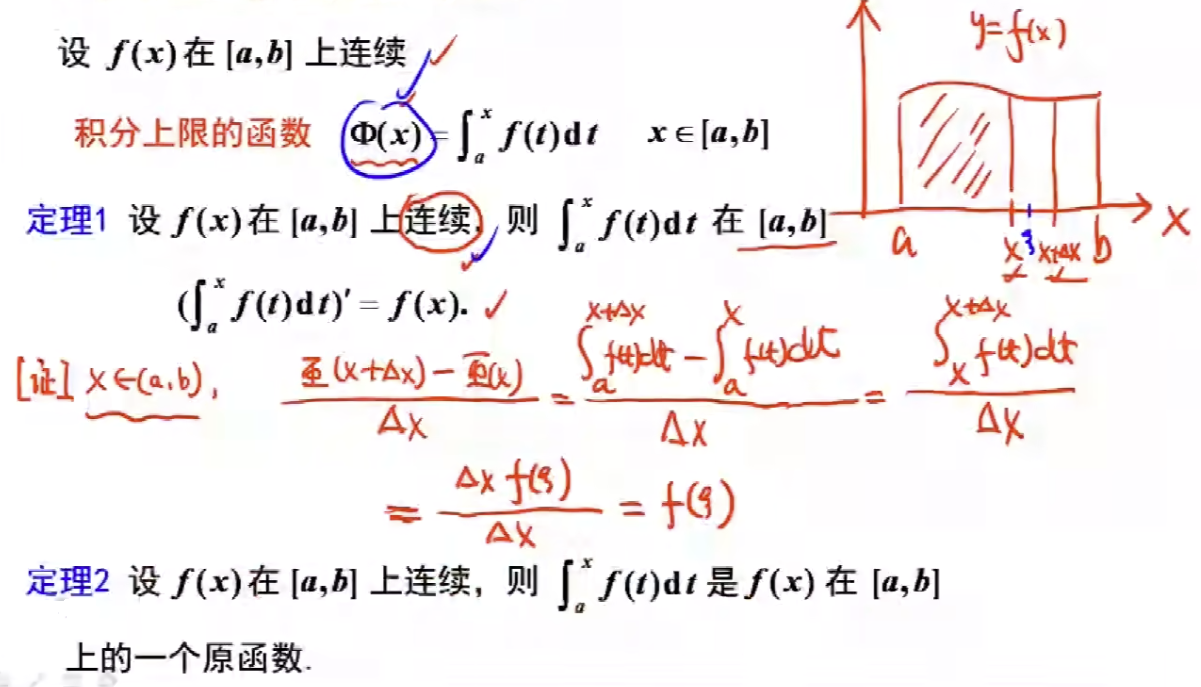
定积分变上下限函数及其导数(积分区间可加性证):
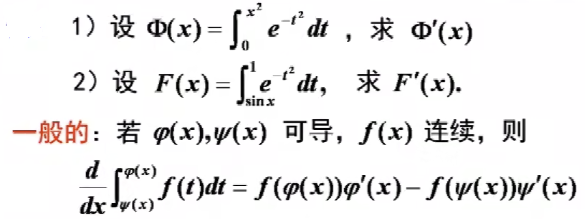
例题1-变上限记得对复合函数求导:

变下限则加负号(交换积分区间)
例题2-积分上限的导数-配合洛必达上下求导:
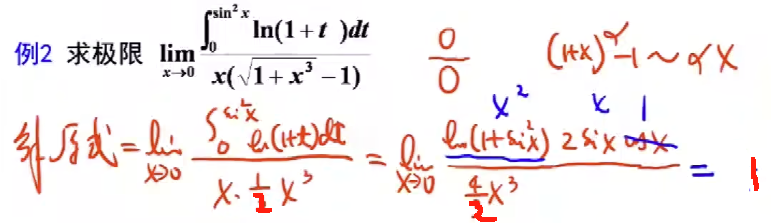
微积分基础公式 #
上下限交换加负号
积分区间可加性
牛顿-莱布尼兹公式(连续函数一定有原函数):

内容小结:

习题 P244: 3,4,5(3),8(8,11,12). 9, 10, 11, 12
定积分的应用 #
能用定积分解决的问题的特称:
- 非均匀连续分布在 [a, b] 上的量
- 所求量对区间有可加性
归元法(元素法)三部曲: - 范围
- 微元: $du = f(x)dx$
- 积分: $U = \int_a^b f(x)fx$
以求曲线 $y^2 = x$ 和 $y = x^2$ 所围面积为例:
- 范围 x ∈ [0, 1] (也可对 y 积分)
- 微元(近似) $dS = [x^{\frac{1}{2}} - x^2]dx$
- 积分 $S = \int_0^1 [x^{\frac{1}{2}} - x^2]dx = \frac{1}{3}$
例题1 - 对 y 积分例子:

例题2 - 参数方程

例题3 - 极坐标方程及其例子

X/Y旋转体体积的公式:
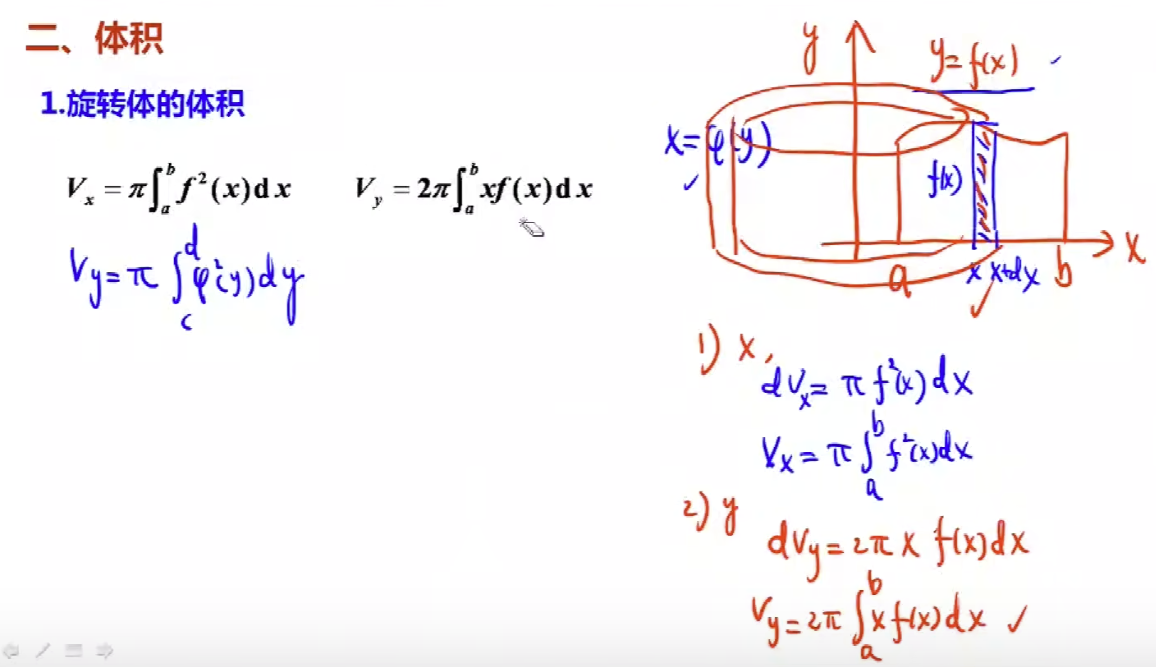
例题5 - 旋转题体积

例题6 - 参数方程+旋转体:

平行截面积为已知的立体的体积 & 例题7:

平面曲线的弧长 & 弧微分:

例题8 - 摆线(最速降线) - 参数方程求弧长
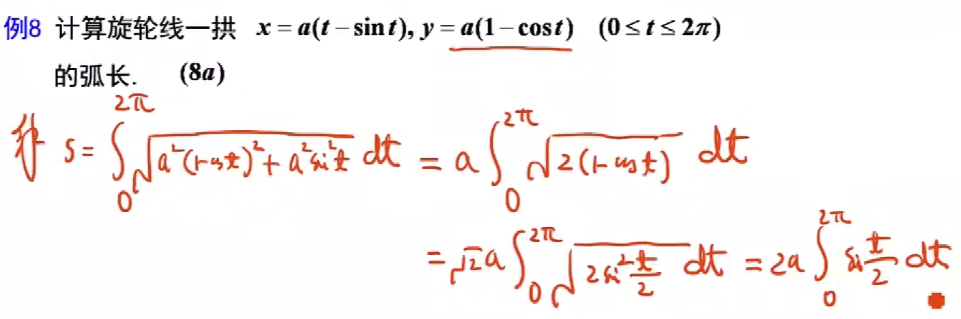
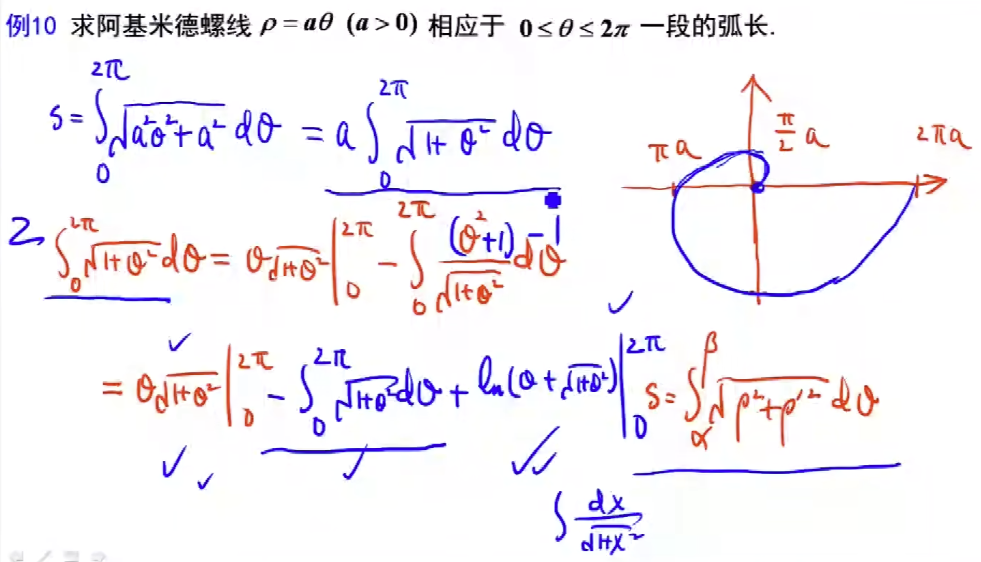
例题9 - 阿基米德螺线 - 极坐标方程求弧长
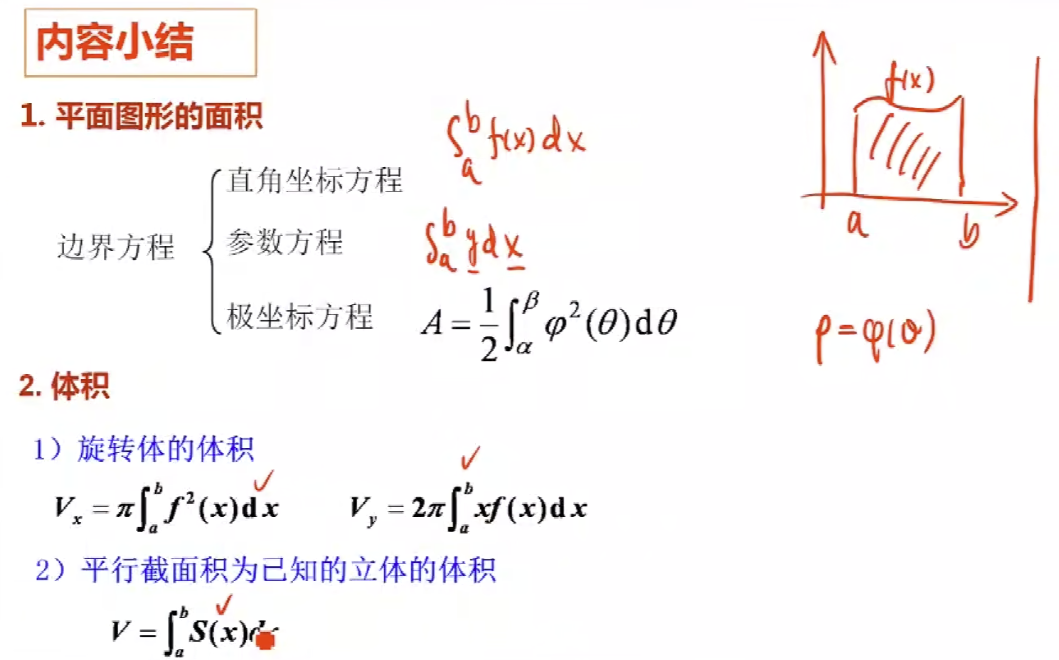
内容小结:

习题P286: 3, 5, 7, 11, 12, 13, 15(3,4), 19, 20, 24, 25
反常积分 #
两种类型 #
无穷限的反常积分(积分区间为无穷区间) #
计算方法: $\int_a^{+\infin}f(x)dx = F(x)|a^{+\infin} = \displaystyle \lim{x \rightarrow +\infin}F(x) - F(a)$
极限存在则收敛, 否则为发散
例题:

无界函数的反常积分(被积函数为无界函数) #
也称为瑕积分, 瑕点可理解为无穷间断点
反常积分的审敛法 #
积分极限不容易直接求出的时候,考虑以下方法:
比较法的一般形式 #
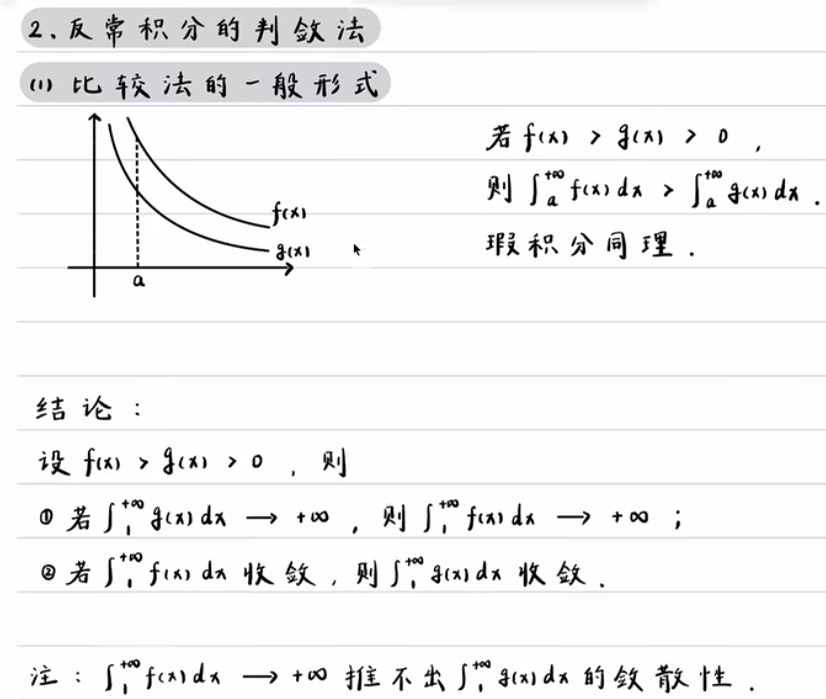
比较法的极限形式 #
- 无穷限型

- 无界函数
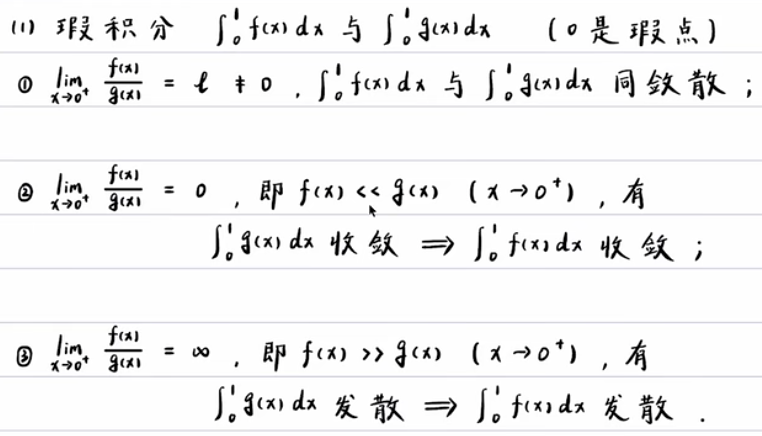
总结: 同阶同敛散
p值审敛法 #

例题 #
问题点: 无穷和瑕点;
只有问题点才会影响敛散性
例题1 - 常规例题:
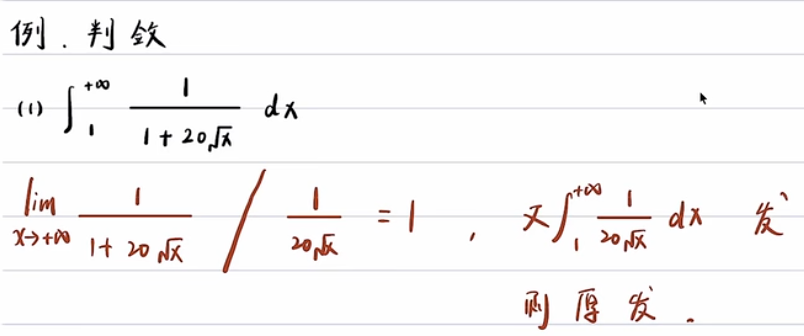
例题2 - 分段, 定积分部分不影响敛散性
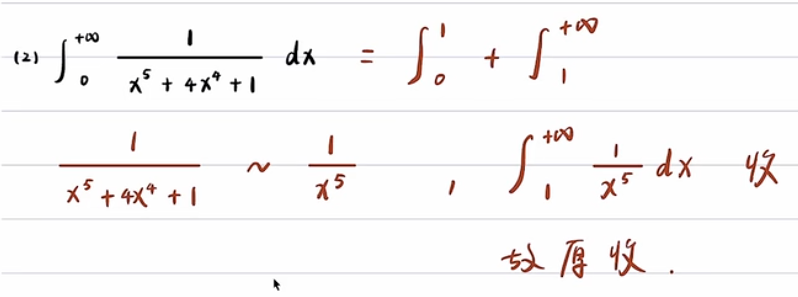
例题3 - 一般审敛法
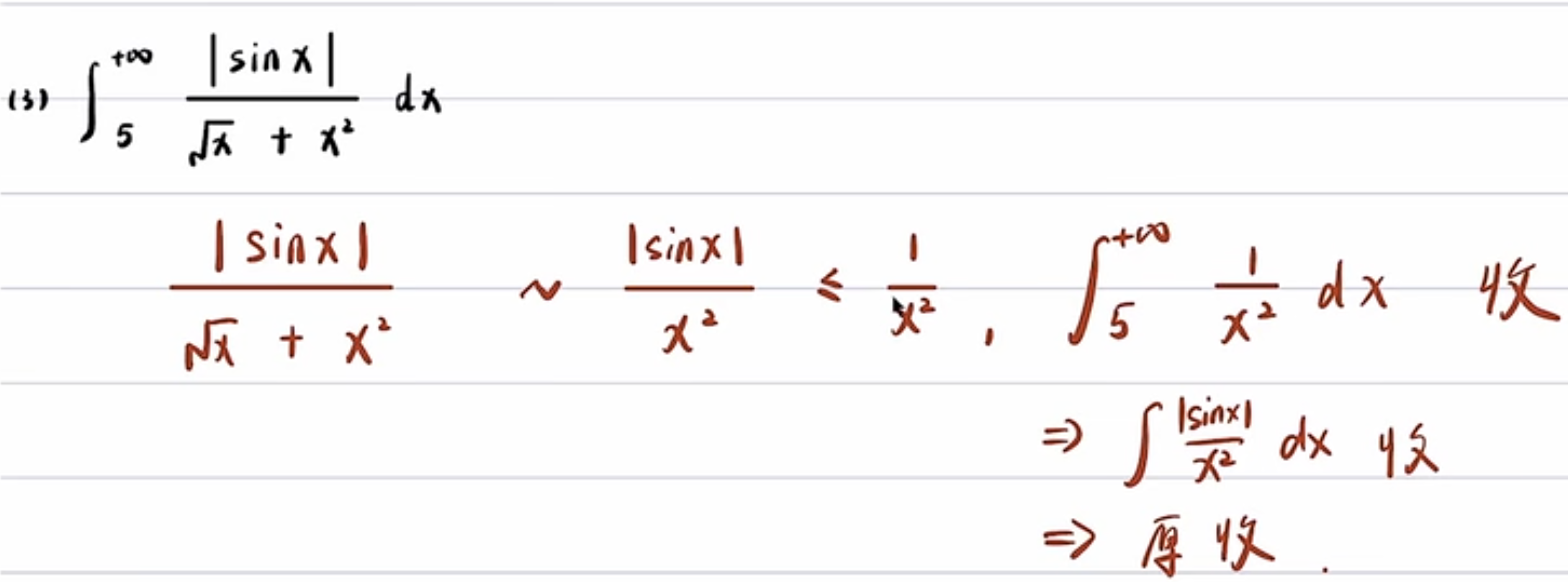
例题4 - 多问题点

真题 #
做题技巧 #
求定积分 #
- 区分区间可变可拆(数一23年14题)
- 无关项可以当常数提出去, 注意判断变量相关性

