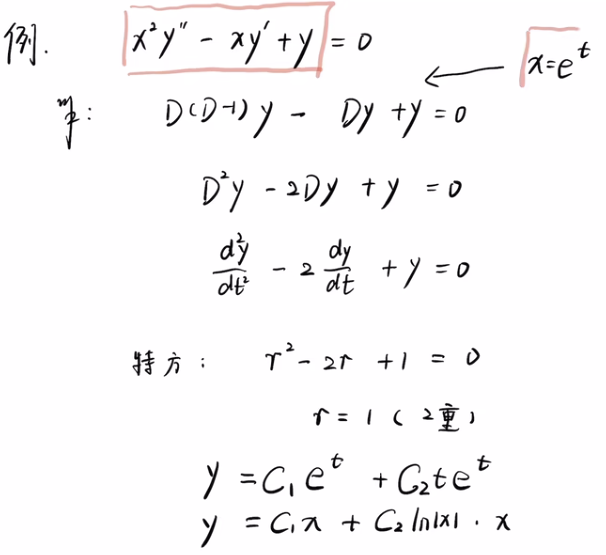微分方程 #
线性:就是指变量的次数为1
齐次:不带常数项(0是任意次的)
拿到方程先分析类型: 线性, 齐次, 可分离变量, 伯努利…(都不是还要考虑x/y对调等)
一阶线性微分方程 #
可分离变量的微分方程:
如果一个一阶微分方程能写成:
$$ \begin{aligned} g(y)dy = f(x)dx \end{aligned} $$
那么原方程就称为可分离变量的微分方程
如: $\frac{dy}{dx} = 2xy^2$ 两边同乘 $\frac{dx}{y^2}$ 后对两边积分得:
$$ \begin{aligned} -\frac{1}{y} = x^2 + C \end{aligned} $$
线性方程通解:

例题 - x/y只是符号, 可任意换元
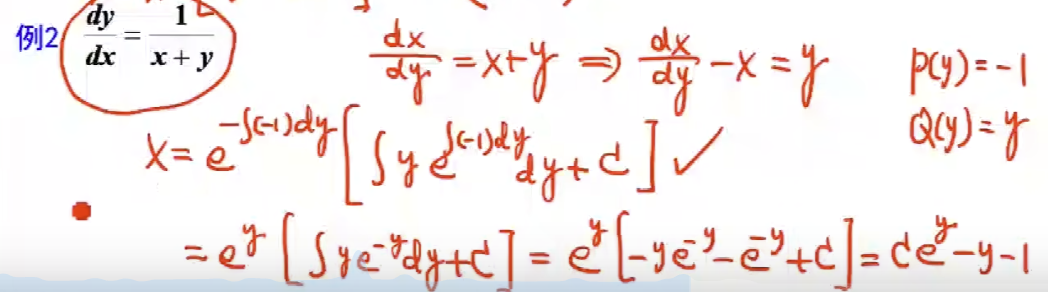
伯努利方程(右侧多出$y^n$, 两边同除掉):

内容小结:

习题P329: 1(3,6,9), 2(5), 7(1, 3), 8(2, 4)
常系数齐次线性微分方程 #
缺: 可降阶的高阶微分方程, 高阶线性微分方程
二阶常系数齐次线性方程 #
扩展: 由刘维尔方程得出特称方程解法:

例题1 - 基础运用:
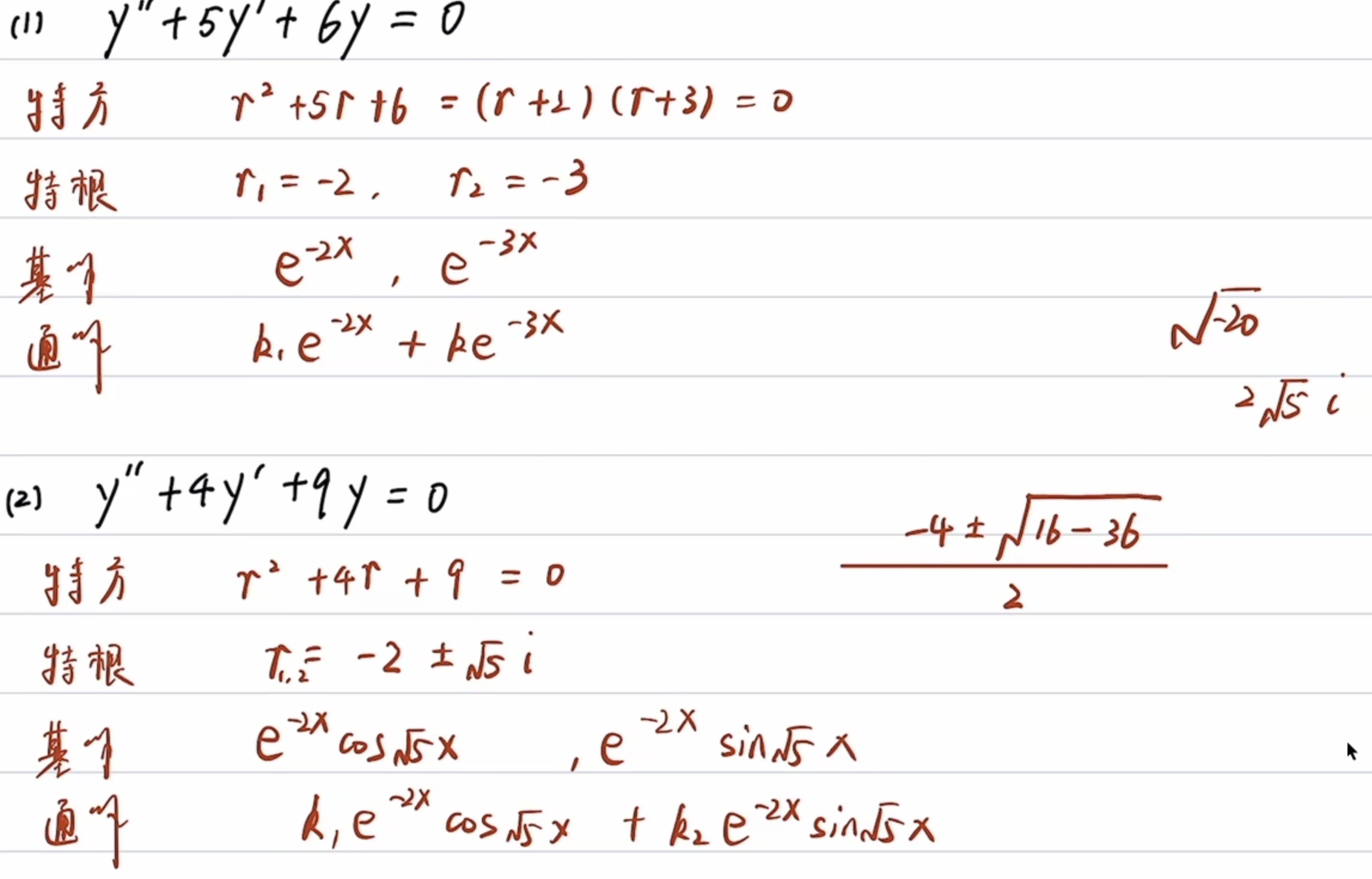
如何推广到高阶:

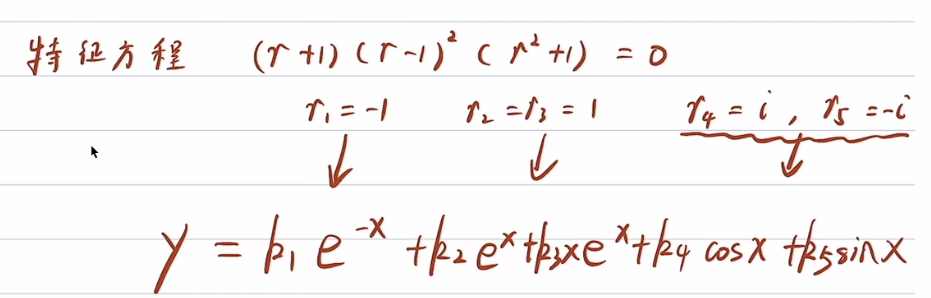
另一种版本的高阶特征方程公式:

习题 P346: 1(3,6,10), 2(2,3,6), 3
常系数非齐次线性微分方程 #
二阶常系数非齐次微分方程 #
$y_非齐次通解 = 齐次通解 + 非齐次特解$
齐次通解之前已经解决,本节重点在于求非齐次特解:
特解求法分两种函数构型:
$f(x) = e^{λx}P_m(x)$ 型 #

第一型求特解例子1(多项式 Ax + B 的次数由 Pm 中 x 的次数得来):
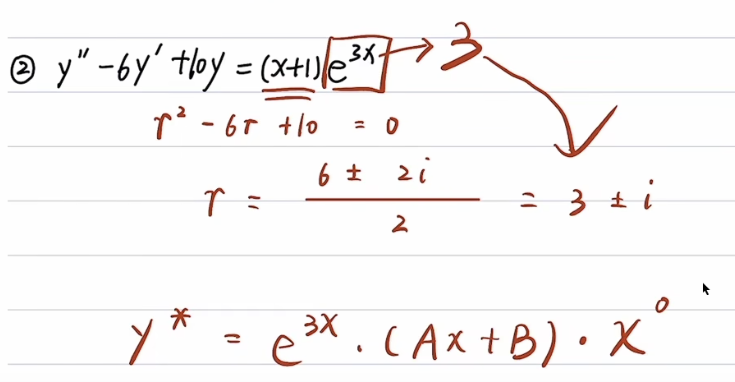
λ 不是解则 k = 0(0重)
第一型求特解例子2:
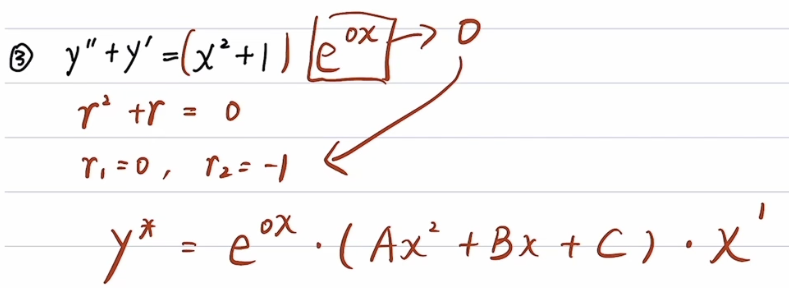
第一型计算非齐次通解例子:
例: 解 $y^{’’} - 3y^{’} + 2y =3xe^{-x}$
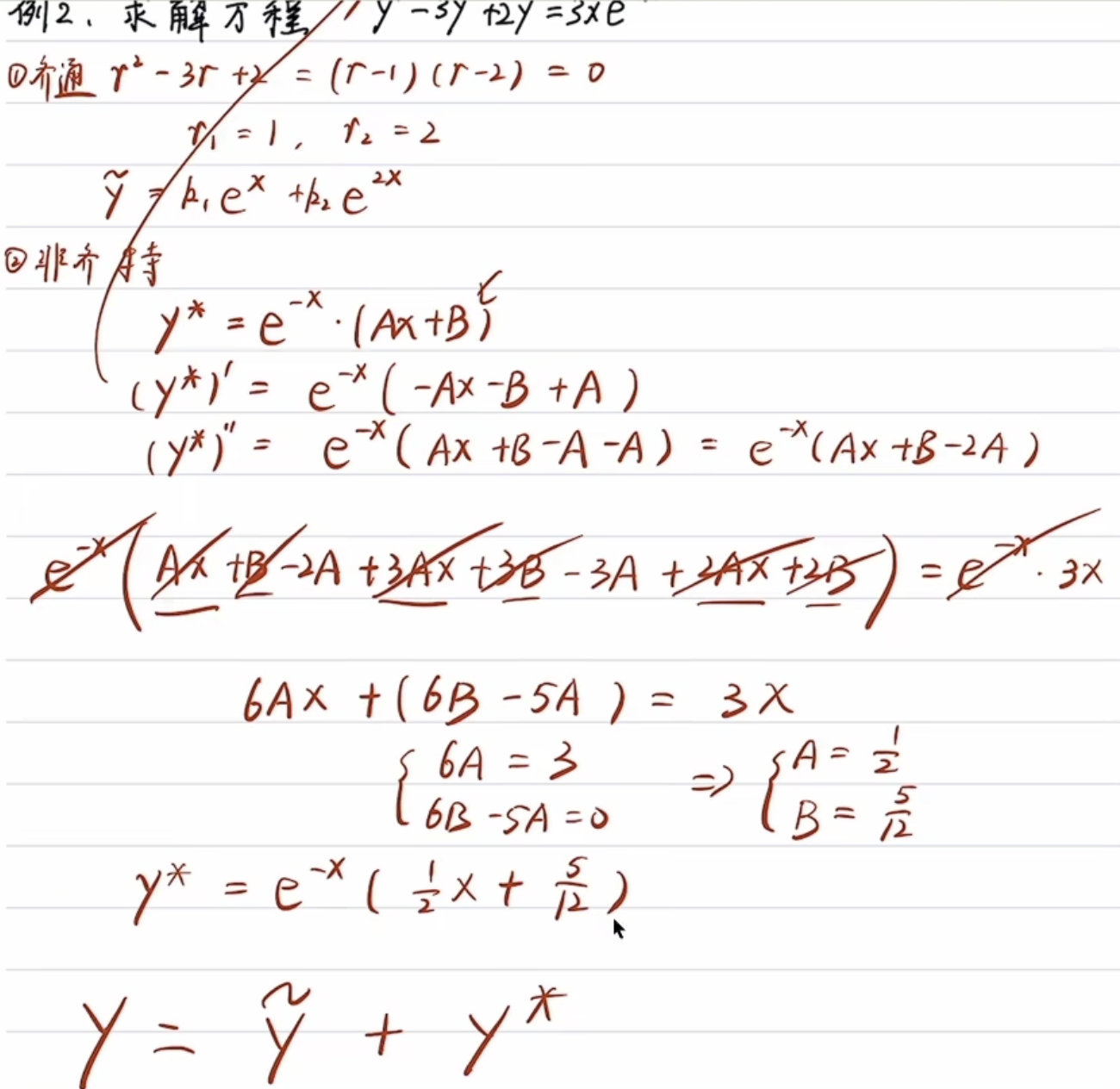
$f(x) = [P_m(x)cosβx + Q_n(x)sinβx]e^{αx}$ 型 (多项式阶数 = max(m, n)) #

第二型求特解例子1:

第二型求特解例子2:
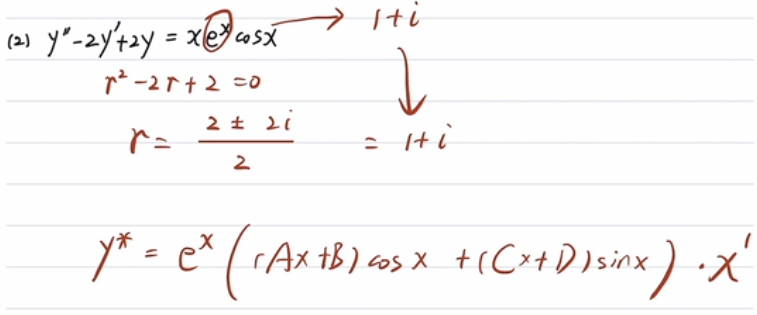
第二型计算非齐次通解例子:

- 叠加方程
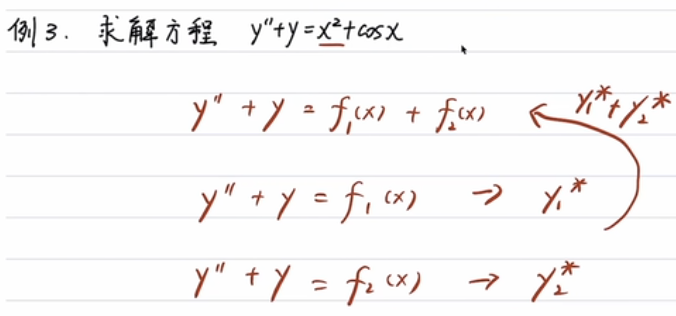
内容小结:

习题P354: 1(1,5,6, 10), 2(2,4), 6
欧拉方程 #
欧拉方程形式: $x^ny^{(n)}$ 的线性组合
以二阶为例: $x^2y^{’’} + pxy^{’} = qy = 0$
欧拉方程推导:
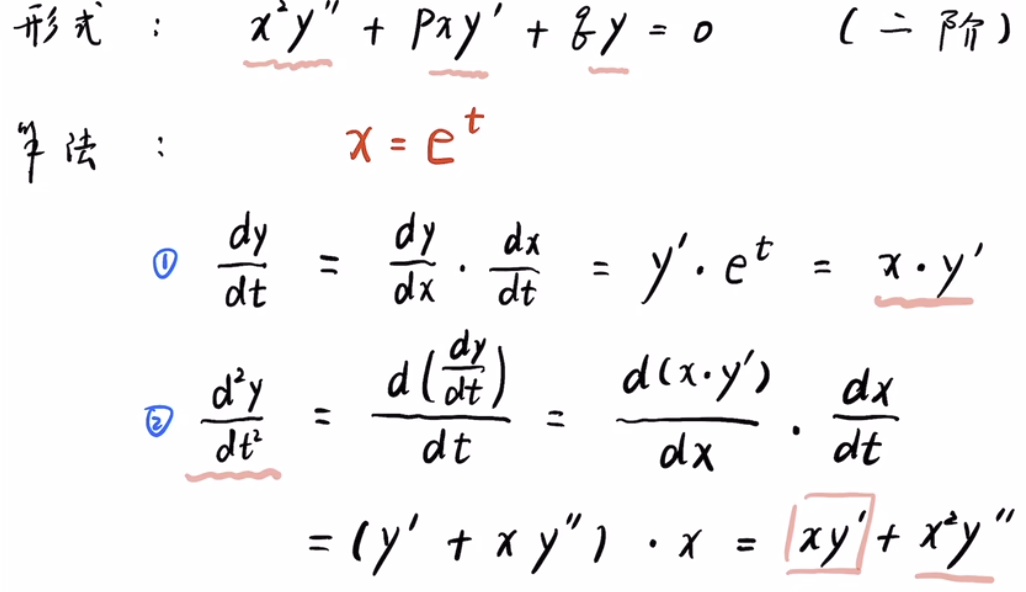
引入微分算子:
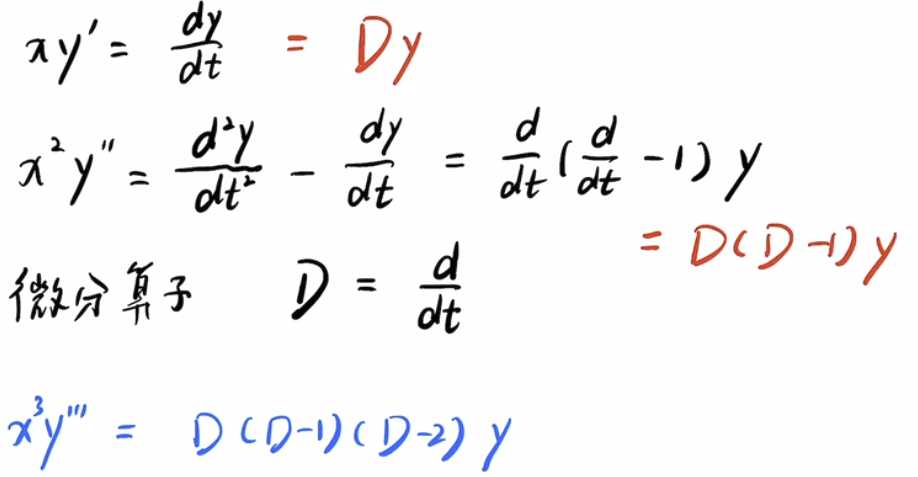
代入后解 n 阶常系数微分方程:
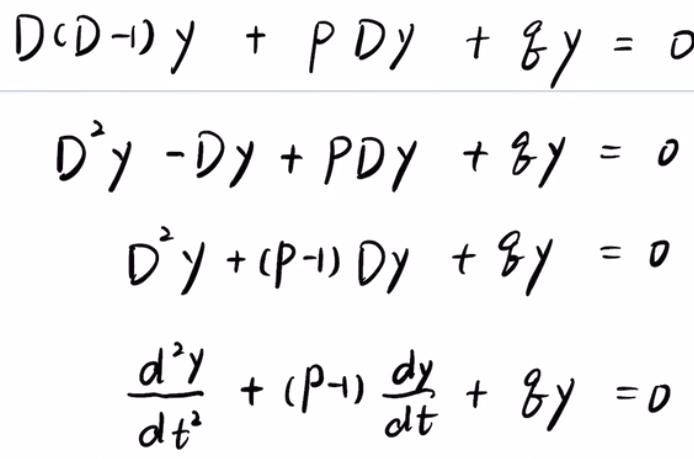
例题(注意不要跳步骤, 尤其最后 $x = e^t$ 需要还原):