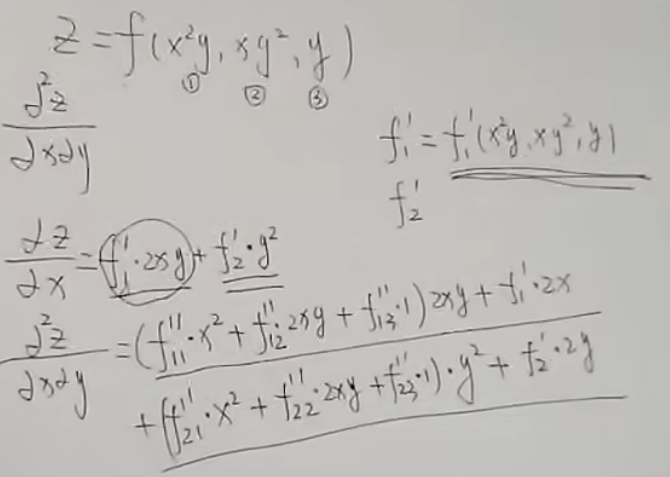多元函数微分法及其应用 #
善于类比:
形式:
一元函数: y = f(x)
多元函数: z = f(x, y)
图形:
一元函数: 线
多元函数 面
邻域(都是定义在去心临域的):
一元函数: 直线
多(二)元函数: 圆
极限: 可选择某一个方向(y = kx) 证明极限不存在, 或者夹逼定理求极限
求连续性: 注意初等函数在其定义域都是连续的, 某点极限等于该点函数值
偏导数 #
多元函数中某一个自变量改变的导数,对应偏增量, 例如: z= f(x, y) x 变, y 不变(两者都变叫方向导数, 对应全增量)
几何意义对应: y 固定时(截面)的相交线在 x => x0 的切线
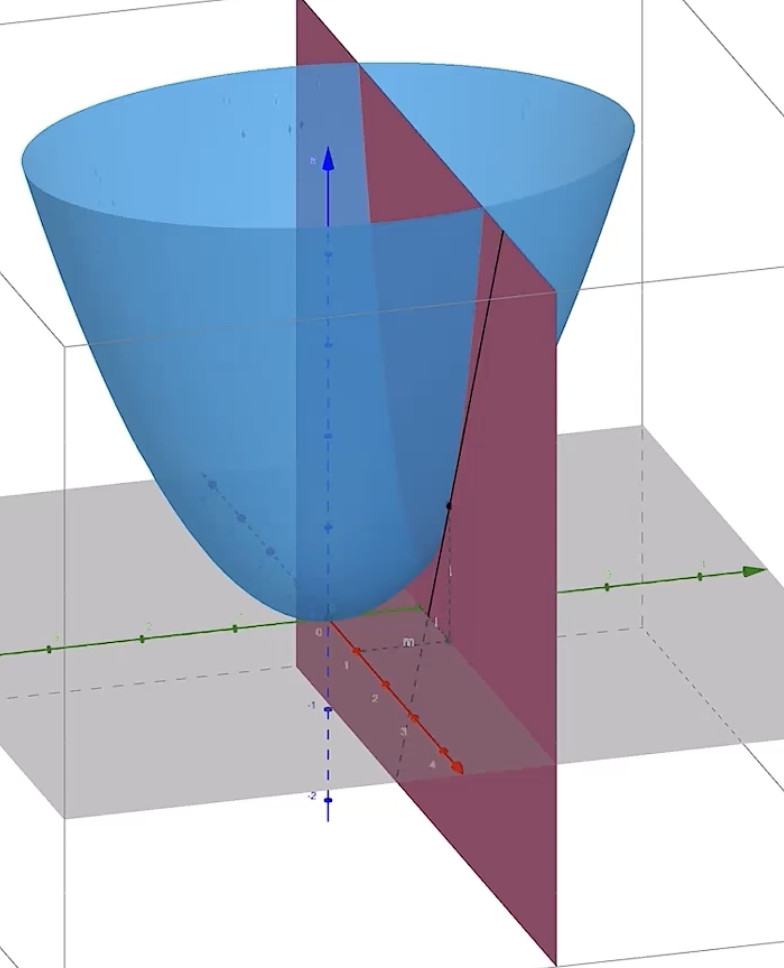
可偏导未必连续: f(x, y) = 1, 定义域: xy = 0;
连续未必可偏导: z = |x|
高阶偏导数 #
按照变量求导次序不同有不同的高阶偏导数
分别对不同变量求导称为混合偏导数, 如果混合偏导数连续那么其值与求导次序无关
全微分 #
可微定义:
一元函数可微: $\Delta{y} = A\Delta{x} + o(\Delta{x})$, $A = f^{’}(x)$
多元函数可微:
对 z = f(x, y) 若全增量:
$\Delta{z} = f(x_0 +\Delta{x}, y_0 + \Delta{y}) - f(x_0, y_0)$
与自变量增量 $\Delta{x}, \Delta{y}$ 有关系:
$\Delta{z} = A\Delta{x} + B\Delta{y} + o(\sqrt{\Delta{x}^2 + \Delta{y}^2})$ ($A=F_x, B = F_y$)
则称 z 在 $f(x_0, y_0)$ 处可微:
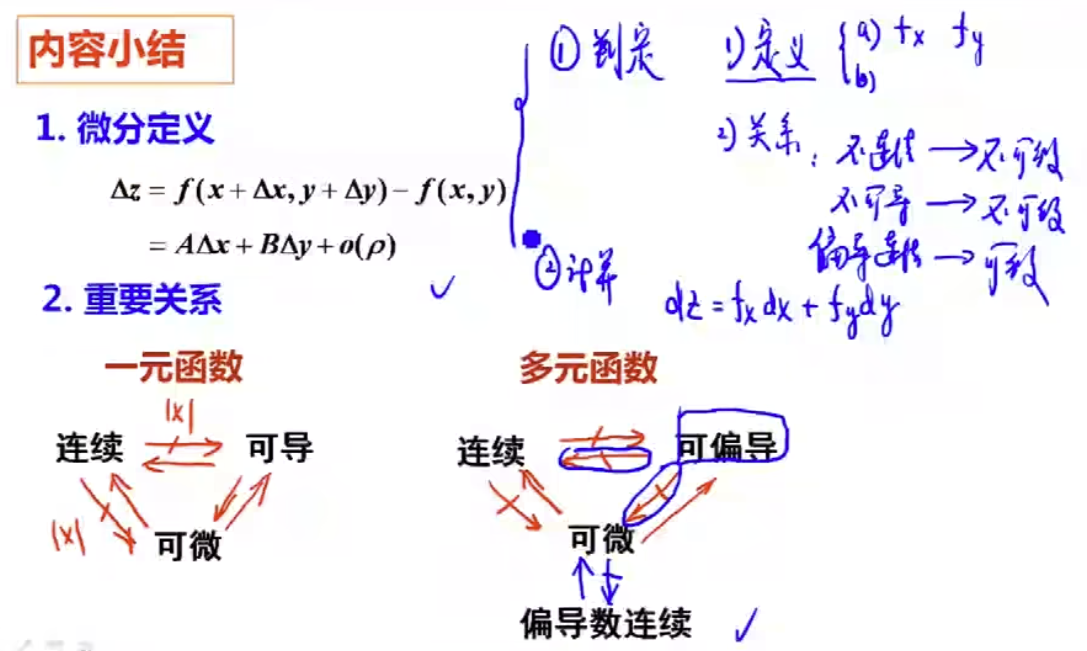
可微必连续(必要条件)
可微必可偏导(必要条件)
偏导数连续则可微(充分条件,平面光滑)
内容小结:
习题 P77: 1(3)(4), 2, 3, 5
多元复合函数微分法(难点) #
以树的方式理解偏导数复合规则(分叉用加, 串联用乘, 单路全导, 多路偏导)
二元抽象复合函数,无论对谁求偏导也无论求几阶偏导,所求的出来的结果函数,永远与原来的函数具有相同的复合结构”,所以原函数是三部分,一阶函数也是三部分
公式:

全微分形式的不变性:

内容小结:

习题P84: 2,4,8,9, 12(1)(4)
二元函数的极值 #
判别法失效, 进一步讨论如何讨论(回归基本定义):

计算示例方法1:
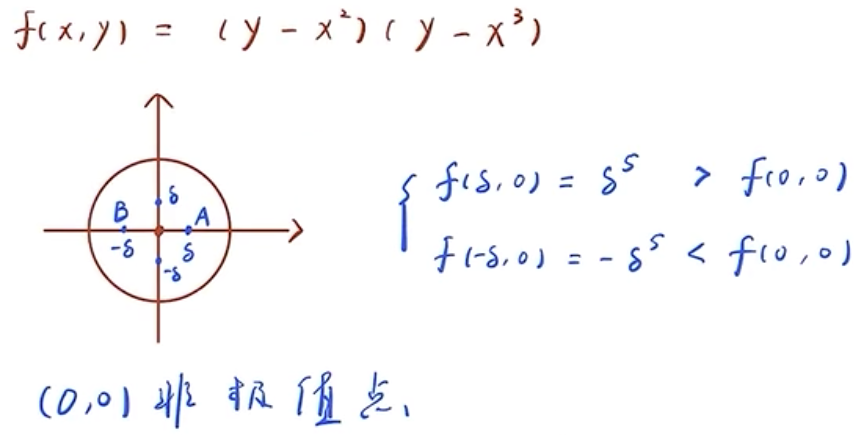
计算示例方法2:

遗漏部分 #
差: 隐函数, 几何, 方向导数与梯度, 多元函数极值, *二元函数泰勒, *最小二乘法